[논문읽기] Are Transformers universal approximators of sequence-to-sequence functions?

🗓 January 30, 2022

Abstract
Keywords & Definitions
Main Text
My Comments & Questions

Abstract

Transformer encoder는 ‘permutation equivariant’한 성질을 갖는 연속인 ‘sequence-to-sequence’ 함수(with compact support)에 대한 universal approximator임을 보인다.
Transformer encoder에다 learnable한 positional encodings를 같이 쓰면 임의의(permutation equivariant하지 않아도) 연속인 ‘sequence-to-sequence’ 함수(with compact domain)를 universally approximate함을 보인다.
Contextual mapping이라는 것을 수식적으로 정의했으며, Transformer Encoder의 multi-head self-attention layer들이 입력 sequence에 대한 contextual mapping을 잘 계산함을 보인다.
(실험도 진행하였으나 여기서는 생략)

Keywords & Definitions

1. Sequence-to-sequence Function

$\mathbb{R}^{d\times n}$에서 $\mathbb{R}^{d\times n}$로 가는 함수를 sequence-to-sequence function이라고 말한다. 정확히는 정의역도 치역도 모두 subset of $\mathbb{R}^{d\times n}$인 함수를 말한다. ($\mathbb{R}^{d\times n}$: the set of all $d\times n$ real matrices)

이때 $d$와 $n$은 각각, Transformer 논문에서 언급하는 embedding 차원과 입력 sequence 길이로 비유된다. 기존 Transformer 논문에서도 거의 같은 표기를 사용했다($d_{\text{model}} = d$). 한 가지 차이가 있다면, Transformer 논문에서는 $n\times d$ 행렬을 쓰는 반면, 이 논문에서는 그 반대($d\times n$ 행렬)를 이용하기 때문에, 행렬의 각 열(column)이 한 input word embedding(혹은 token)으로 비유된다. 안그래도 이 논문에서 계속해서 $d\times n$ 행렬 $X$를 input sequence라고 칭한다.

Sequence-to-sequence 함수의 연속성 정의
Sequence-to-sequence function이 행렬을 받아 행렬을 내뱉는 함수이다 보니 연속성도 잘 정의되어야 한다. 논문에서는 $\mathbb{R}^{d\times n}$에 entry-wise $\ell^p$ norm($|\cdot|_p$)과 그에 대한 norm topology를 주고 그 위에서 연속성을 정의하는 것으로 보인다. 이때 $p$의 값은 $1\le p<\infty$.
함수 간의 거리(function metric)
함수끼리 얼마나 가까운 지를 나타내기 위해 function 사이의 distance를 정의한다. 즉 sequence-to-sequence function space의 metric $d_p$을 쓰자면 다음과 같다.
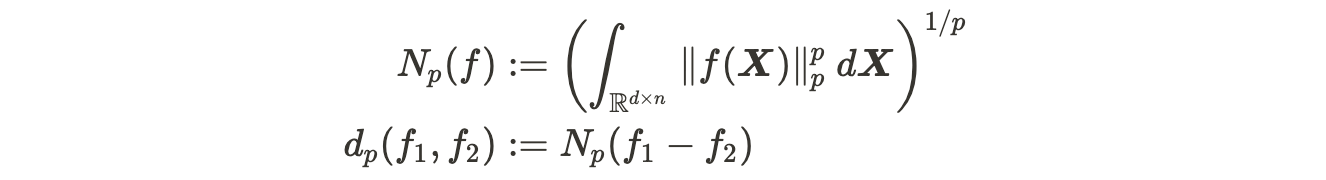
(Usual한 $L^p$ function norm을 이용해서, 논문에 있는 표기와 조금 다르게 적어보았다.)
- Note: 논문에서는 언제나 compact domain, compact support를 가정하기 때문에, $N_p(f)$가 무한대로 발산할 걱정은 하지 않아도 될 것 같다.

2. Permutation Equivariant

Permutation matrix란
Permutation matrix는 각 행과 각 열마다 1이 딱 하나씩 있는 정사각행렬이다. 어떤 행렬 $A\in \mathbb{R}^{m\times n}$에 Permutation matrix $P$를 곱하면 $A$의 행 또는 열의 순서를 뒤죽박죽 섞어 놓은 것과 같다. 좀 더 정확히는, (1) $P\in \mathbb{R}^{n\times n}$이라면 $AP$는 $A$의 열들의 순서를 섞어놓은 행렬이 되고, (2) $P\in \mathbb{R}^{m\times m}$이라면 $PA$는 $A$의 행들의 순서를 섞어놓은 행렬이 된다. 예를 들자면 다음과 같다.
\[\begin{pmatrix} 1&2&3 \\ 4&5&6 \\ 7&8&9\end{pmatrix}\begin{pmatrix} 0&1&0 \\ 0&0&1 \\ 1&0&0\end{pmatrix} = \begin{pmatrix} 3&1&2 \\ 6&4&5 \\ 9&7&8\end{pmatrix}\]
참고로 이러한 permutation matrix는 언제나 orthogonal하다: $P^TP=PP^T=I$. (P가 행/열의 순서를 어떻게 섞는지 생각해보자.)

임의의 $X\in \mathbb{R}^{m\times n}$와 임의의 permutation matrix $P\in \mathbb{R}^{n\times n}$에 대해서, Sequence-to-sequence function인 $f$가 $f(XP)=f(X)P$를 만족하면 이러한 함수가 permutation equivariant하다고 말한다.

Sequence의 순서를 뒤섞는 일을 함수에 대입하기 전에 하나 후에 하나 달라지지 않는 함수를 말한다고 보면 된다.

참고로 논문에서는 각각의 transformer (encoder) block이 permutation equivariant한 sequence-to-sequence function임을 증명한다. (Claim 1)

3. Universal Approximation

딥러닝 이론의 출발점이라고 할 만한 정리로, Neural network의 expressive power에 대해 알려주는 정리인 ‘universal approximation theorem’이 있다. 이것의 내용을 요약하자면 다음과 같다.

Hidden layer가 1개 있는 neural network만 가지고도 아무런 연속함수(with compact support)를 임의의 (아주 작은) 오차로 근사할 수 있다. (단! network의 width에는 제한이 없으며, 중간에 있는 activation function은 다항함수가 아님.)

이처럼, Universal Approximator는 ‘임의의 정확도로 엄청 많은 함수들을 근사할 수 있’는 모델을 두고 하는 말이다. 이후로도 universal approximation에 대한 다방면의 연구가 이루어졌는데, 이는 여기서 소개하는 논문의 section 1.2 related works & notation에 잘 소개되어 있다.

4. Contextual Mapping

논문에 따르면, Transformer가 높은 성능을 보여주는 이유가 보통 ‘contextual mapping’을 잘 계산하기 때문이라고 평가된다고 한다. 즉, 각각의 문맥을 서로 잘 구분하는 능력이 탁월하다고 보는 것이다.

논문에서는 Trasformer의 이런저런 universal approximation 능력을 증명하려 하는데, 그 과정 중에 ‘(multi-head) self-attention layers가 contextual mapping을 잘 계산한다’는 것을 증명하는 게 정말 중요한 중간 과정이라고 한다. 이를 위해 논문에서는 contextual mapping의 개념을 아예 수식적으로 정의해버린 뒤에 이를 증명에 이용한다. 논문에서 주어진 정의는 다음과 같다.

즉 contextual mapping은 길이 $n$인 input sequence를 받아 $n$개의 값 (혹은 $n$차원 열벡터)를 내놓는 함수로 정의된다. 이때 한 문장(sequence) 안의 단어들은 서로 다른 역할을 하므로 각각 다른 context값(contextual mapping의 entry)이 매겨진다(1번 조건). 게다가, 같은 단어라도 다른 문장에서는 다른 의미로 해석된다는 의미에서, 서로 다른 두 input sequence(L, L’)에 대한 contextual mapping에 있는 모든 (총 2n개의) entry들은 전부 다르게 매겨진다(2번 조건).

집합 $\mathbb{L}$이 유한집합으로 설정된 이유는 (내 생각에는)
Vocabulary의 크기도 유한하고 sequence 길이도 유한하므로 만들 수 있는 input sequence의 개수는 유한하다. Sequence들의 집합과 대응되는 집합이 $\mathbb{L}$과 비슷한 것이라면, $\mathbb{L}$을 유한집합이라고 놓아도 괜찮을 것이다. (이 조건이 필수인지는 증명을 더 들여다봐야..)

Main Text

1. Universal Approximator임을 보이기 힘든 이유

너무 많아 보이는 Parameter sharing. Self-attention layer와 feed-forward layer 모두, token끼리 공유하는 parameter의 수가 매우 많다.
너무 적어 보이는 token-wise interaction. Self-attention layer의 특성상 pairwise dot-product로만 token 사이의 interaction을 잡아낸다.

(둘째 이유는 그럴 만하다고 보이는데, 첫째 이유는 아직 잘 이해하지 못했다.)

논문에서는 위의 두 이유로 인해 transformer encoder 자체가 나타낼 수 있는 sequence-to-sequence 함수의 종류에 제한이 있다고 보며, 이를 trainable한 positional encoding으로 해결한다.

❓ 일반적으로, Parameter sharing이 많을수록 universal approximator가 되기 어려운 이유는 무엇일까?

2. 논문에서 본 Transformer

아래는 논문에서 사용한 transformer block에 대한 식이다.

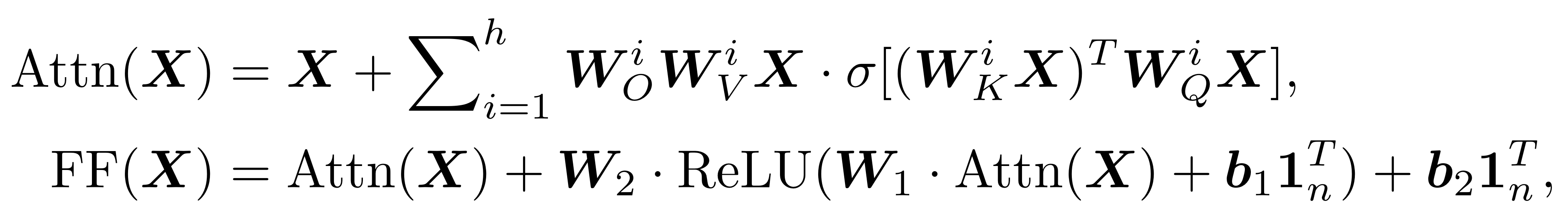
잘 알려져 있듯, transformer encoder block은 multi-head self-attention layer(’Attn’)와 token-wise feed-forward layer(’FF’)라는 두 (sub-)layer로 나뉜다.

2.1. 기존 Transformer 논문과의 공통점

수식에서 확인할 수 있듯 residual connection은 그대로 살려두었다.

2.2. 기존 Transformer 논문과의 차이점

해석을 간단히 하기 위해 layer normalization은 뺐다고 한다.
Self-attention layer 식을 보면 기존 논문에서는 볼 수 없던 시그마($\sum$) 기호가 보인다. 원래 transformer 논문에서는 attention head들을 concatenate하는데, 이러한 concatenation을 수식적으로는 저렇게 표현할 수 있다고 한다. 즉 의미가 다른 식이 아니다.
Self-attention layer의 소문자 시그마 함수($\sigma(\cdot)$)는 (column-wise) softmax를 가리킨다. 그런데 기존 논문에서는 scaled dot-product attention을 사용하는 반면 여기서는 그냥 dot-product attention을 쓰는 것처럼 보인다. 사실 $\boldsymbol{W}_K$나 $\boldsymbol{W}_Q$같은 parameter들이 그 scaling factor($\frac{1}{\sqrt{d_k}}$)를 학습하면 그만이다.

❓ Layer normalization을 빼도 괜찮은 이유는 무엇일까?

2.3. Positional encoding

Trainable한 positional encoding이 없는 순수한 transformer block은 오직 ‘permutation equivariant’한 종류의 함수만을 잘 근사할 뿐이다. 그러나 positional encoding을 도입함으로써 이러한 함수 종류의 제한 없이 아무런 sequence-to-sequence 함수(with compact domain)을 잘 근사할 수 있게 된다.
Positional encoding $\boldsymbol{E}$ 역시 $d\times n$ 크기의 real matrix로 정의된다. Transformer block을 함수 $g$로 쓴다면, positional encoding이 도입된 transformer block은 input sequence $\boldsymbol{X}$에 대해 $g(\boldsymbol{X}+\boldsymbol{E})$라고 쓸 수 있다.
논문에서는 이 $\boldsymbol{E}$가 trainable하다고 가정하므로 아무렇게나 설정할 수 있다. 실제로, 함수들의 domain이 compact함을 가정해서 input sequence가 $\boldsymbol{X}\in [0,1]^{d\times n}$ 가 되도록 한 뒤, positional encoding을 나타내는 행렬을 임의로 다음과 같이 정의한다. (Appendix C 참고)

\[\boldsymbol{E} = \begin{pmatrix} 0&1&2&\cdots&n-1\\0&1&2&\cdots&n-1\\\vdots&\vdots&\vdots&&\vdots\\0&1&2&\cdots&n-1\end{pmatrix}\]

3. 주요 결과 (2가지)

논문이 주장하는 두 가지 중요한 결과는 Abstract에서 소개한 처음 두 줄과 같다. 여기서는 더 자세한 서술을 소개한다.

Theorem 2. (임의의 $\epsilon>0$와 $1\le p < \infty$에 대해) 함수 $f$가 다음의 조건을 만족한다고 하자.
$f$는 sequence-to-sequence 함수.
$f$의 support는 compact.
$f$는 연속(w.r.t. entry-wise $\ell^p$ norm).
$f$는 permutation equivariant.
그러면 다음 조건을 만족하는 Transformer network $g$가 존재한다.
$g$는 $(h,m,r)=(2,1,4)$를 만족.
$d_p (f,g ) \le \epsilon$.

참고: Transformer network란, 같은 Transformer block을 여러 개 쌓은 것이다. 또 위에서 쓰인 h, m, r은 각각 다음과 같은 것을 나타내는 기호다.

문자	뜻
$h$	attention head의 개수
$m$	attention head의 크기
$r$	feed-forward layer의 hidden 차원 (=$d_{ff}$)

Theorem 3. (임의의 $\epsilon>0$와 $1\le p < \infty$에 대해) 함수 $f$가 다음의 조건을 만족한다고 하자.
$f$는 sequence-to-sequence 함수.
$f$의 domain은 compact.
$f$는 연속(w.r.t. entry-wise $\ell^p$ norm).
그러면 다음 조건을 만족하는 Transformer network $g$ with (trainable) positional encoding $\boldsymbol{E}$가 존재한다.
$g$는 $(h,m,r)=(2,1,4)$를 만족.
$d_p (f,g ) \le \epsilon$.

거의 모든 것이 Theorem 2와 동일하지만, Transformer network에는 positional encoding이 추가됐고, 대신 근사하려는 sequence-to-sequence 함수의 permutation equivariant 조건이 사라졌다.

$(h,m,r)=(2,1,4)$를 쓰는 이유? (너무 작은 block 아닌가?)
Attention head가 2개밖에 없고, 그 크기도 겨우 1이고, 심지어 feed-forward layer의 hidden 차원이 4밖에 안 되는 작은 Transformer block은 실질적으로 쓰이지 않는다. 그러나 이러한 Transformer block을 이용한 이유는 단지 단순화가 증명을 쉽게 해주기 때문만은 아니다.
더 큰 모델은 자명하게 expressive power가 더 크기 때문이다. 실질적으로 쓰이는 transformer block은 훨씬 더 많은 parameter를 쓸 텐데, 그런 model은 논문에서 쓰이는 매우 작은 transformer block에 비하면 당연히 더욱더 많은 함수들을 표현할 수 있을 것이다. 그러니 이렇게 작은 스케일로 문제를 축소시켜서 문제를 풀어도 충분하다.

❓ 위의 두 정리는 universal approximation의 측면에서 매우 유의미한 결과를 내고 있다. 그러나 모두 존재성 정리인 탓에, 훈련 과정에서 transformer가 ‘우리가 원하는 함수’를 실제로 잘 근사할 수 있는지는 말해주지 않는 게 분명하다. 이것이 가능한지는 어떻게 연구해야 할까?/ 어떻게 연구되고 있을까?

4. 어떻게 증명하나?

Theorem 2와 Theorem 3의 증명은 매우 유사하며, 본문에서는 Theorem 2의 증명과정을 요약하여 설명한다. 세 단계로 나누어 임의의 continuous, permutation equivariant, sequence-to-sequence function $f$ with compact support를 적절한 Transformer network로 근사한다. 그 로드맵은 다음과 같다.

4.1) $f$를 piece-wise 상수함수로 근사하기

상수함수라고 해서 f가 갑자기 real-valued가 되는 것이 아니다. 여기서의 상수함수 역시 행렬을 받아 행렬을 내뱉는 함수인데, 함숫값으로서의 행렬이 고정되어 있으면 상수함수인 것이다.

4.2) Piece-wise 상수함수를 ‘modified’ Transformer network로 근사하기

‘Modified’ Transformer란, 기존의 Transformer에서 쓰이던 (column-wise) softmax 함수($\sigma$)는 column-wise hardmax($\sigma_H$)로 대체하고, FF의 activation function으로 쓰이던 ReLU는 또다른 특이한 함수($\phi \in \Phi$, 자세한 정의는 아래에)로 대체한 것이다.

$\Phi$의 정의:
The set of all piece-wise linear functions with at most three pieces, where at least one piece is constant. (p.9)

이 부분을 증명하기 위해, 논문에서는 modified Transformer의 layer 순서를 뜯어고치는 일을 하는 것으로 보인다. Residual connection을 이용하면, self-attention과 feed-forward layer를 번갈아 적용하는게 아니라 self-attention만 쭉, 혹은 feed-forward layer만 쭉 이어 합성한 것을 활용할 수 있다고 한다.

(….) we note that even though a Transformer network stacks self-attention and feed-forward layers in an alternate manner, the skip connections enable these networks to employ a composition of multiple self-attention or feed-forward layers. (중략) self-attention and feed-forward layers play in realizing the ability to universally approximate sequence-to-sequence functions: 1) self-attention layers compute precise contextual maps; and 2) feed-forward layers then assign the results of these contextual maps to the desired output values. (p.6)

❓ Modified Transformer network의 layer 순서를 뒤바꾸어 같은 종류의 layer만 이어붙일 수 있는 이유가 구체적으로 무엇일까? 여기에 skip connection은 어떤 역할을 할까?

4.3) Modified Transformer network를 Transformer network로 근사하기

앞에서 대체했던 softmax와 ReLU를 원래대로 돌려놓는 작업이라고 보면 될 것 같다.

5. 몇 개의 block을 쌓아야 하나?

Theorem 2는 결과적으로 몇개의 Transformer block을 쌓아야 하는지 보여준다. 논문에서 제시하는, permutation equivariant 함수를 잘 근사하기 위해 필요한 (h,m,r)=(2,1,4) Transformer block은 총 $O(n(1/\delta)^{dn}/n!)$개다. 또한, positional encoding까지 더해 좀 더 광범위한 sequence-to-sequence 함수를 잘 근사하기 위해서 필요한 block은 $O(n(1/\delta)^{dn})$개다.

이때 $\delta$는 Theorem 2/3의 증명 1~2단계에서 쓰인 piecewise constant function의 domain을 구분하는 grid를 이루는 (hyper-)cube의 한 변의 길이이며, 충분히 작음을 가정해야 한다. (증명과정에 따르면, $O(\delta^{d/p} ) \le \epsilon/3)$

❓ 논문에서는 증명을 위해 아주 작은 transformer block을 이용하고 있다. 만약 이 transformer block의 크기를 키운다면 필요한 block의 수는 줄어들까? (아마 $d$와 $n$에 따른 complexity에는 크게 차이가 있지 않을 것 같다. $h$, $m$, $r$ 등의 값은 $d$나 $n$의 값과는 관련이 없으므로.)

My Comments & Questions

선형대수학을 꽤나 쓰는 논문이지만 실상은 엄청나게 해석학스러운 논문이었다. 해석학1때 Weierstrass Approximation Theorem(compact domain에서 연속함수를 다항식으로 임의의 정확도로 근사하기) 배웠던 것이 새록새록…
위에서 던졌던 질문들은 내가 논문을 읽으면서도 끝까지 이해하지 못했던, 혹은 스스로 100% 만족스럽게 대답하지는 못했던 질문들이다. 다시 모아보자.