Convergence and Implicit Bias of Gradient Descent on Continual Linear Classification

Abstract

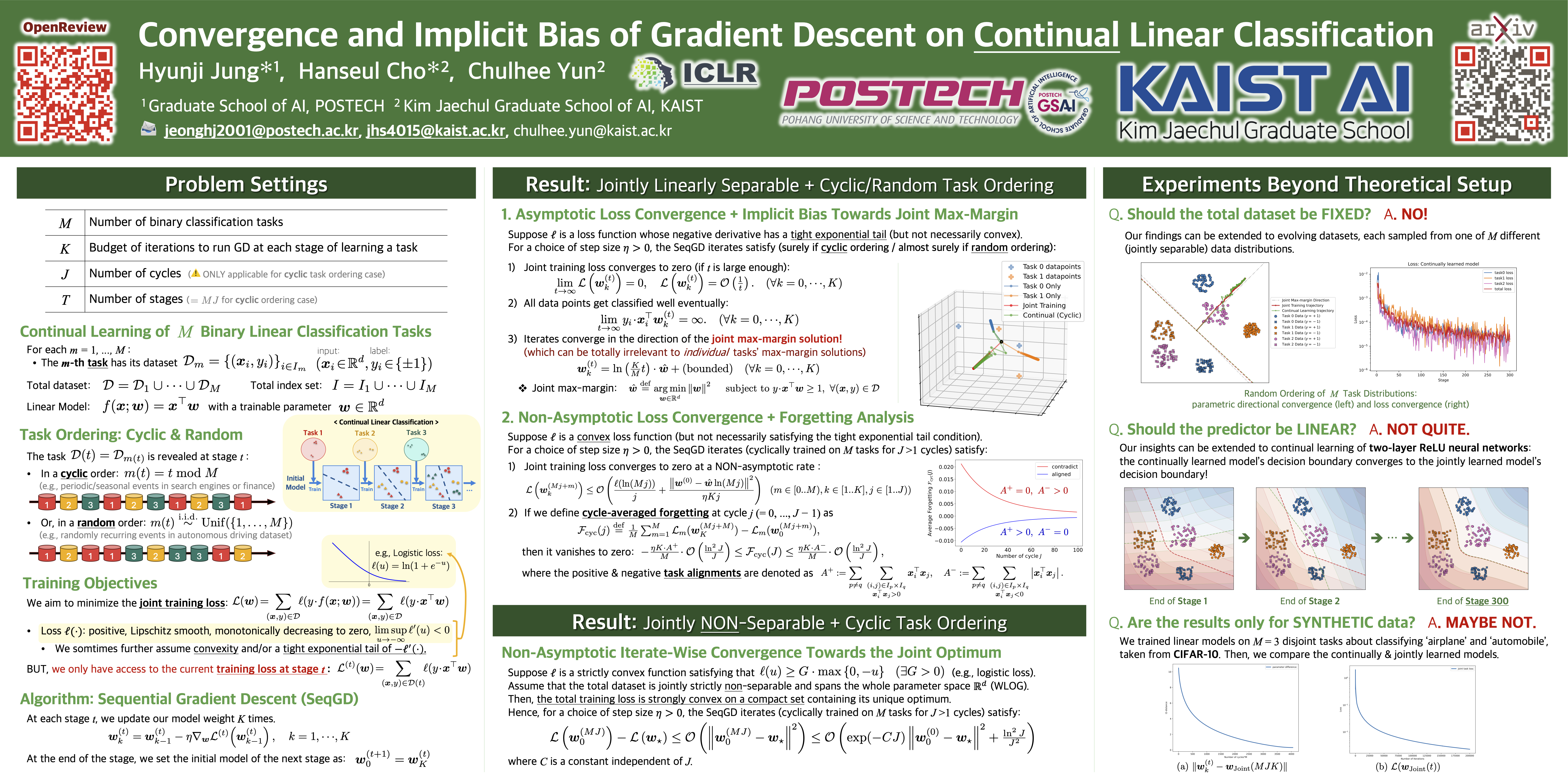
We study continual learning on multiple linear classification tasks by sequentially running gradient descent (GD) for a fixed budget of iterations per task. When all tasks are jointly linearly separable and are presented in a cyclic/random order, we show the directional convergence of the trained linear classifier to the joint (offline) max-margin solution. This is surprising because GD training on a single task is implicitly biased towards the individual max-margin solution for the task, and the direction of the joint max-margin solution can be largely different from these individual solutions. Additionally, when tasks are given in a cyclic order, we present a non-asymptotic analysis on cycle-averaged forgetting, revealing that (1) the task alignment is closely tied to catastrophic forgetting and backward knowledge transfer and (2) the amount of forgetting vanishes to zero as the cycle repeats. Lastly, we analyze the case where the tasks are no longer jointly separable and show that the model trained in a cyclic order converges to the unique minimum of the joint loss function.